В нашем обыденном понимании искусственный интеллект (ИИ) — это некое подобие самого человека. Это созданное его руками существо, которое будет способно чувствовать, творить что-то новое и понимать. Поэтому проблема ИИ отчасти философская - человек сам не до конца понимает природу всех психофизических процессов, которые с ним происходят. Все чувства, переживания и терзания души трудно будет смоделировать с помощью машины, да и творить что-то совершенно новое компьютер, я думаю, научится не скоро. Но есть одна способность, которой ученые стремятся одарить современные машины — это способность к пониманию. Что есть понимание?
Давайте для наглядности разберем случай [1], который произошел при тестировании шахматной программы «Deep Thought», обыгрывающей шахматных чемпионов. В этом тесте программе была заранее введена нестандартная позиция, которая показана на рис.1. Компьютер, играя белыми, совершил грубейшую ошибку. Даже людям, которые играют всего несколько лет, ясно, что такую позицию можно свести к ничьей, однако, программа пешкой съедает ладью и проигрывает. Этот пример говорит о том, что, зная определенные алгоритмы, программа может обыгрывать людей и даже чемпионов, но она в целом, не обладает пониманием принципов игры, а просто действует согласно определенным предписаниям. Другой пример состоит в том, что некоторые математические теоремы просто невозможно вывести с применением вычислительных методов, то есть компьютеры в силу применяемых ими методов физически не могут решить эти проблемы. Получается, созданная нами машина никогда не будет действительно разумной, в том смысле, что она никогда не будет способна понимать, что она делает и действовать на основе этого понимания. Но нельзя однозначно сказать, что создание ИИ невозможно — просто он не будет «машиной» в современном понимании этого слова. Для работы ИИ в нем должны протекать такие же процессы, которые ответственны за возникновение нашего человеческого сознания. Однако познания наук о человеческом мозге еще не позволяют познать его природу во всем его многообразии. Мы можем, на основании достижений современной науки, лишь предположить, что наиболее вероятно будет включать в себя ИИ. В одной замечательной книге [1], посвященной этой проблеме, говорится, что зачатки сознания необходимо искать на границе между квантовыми и классическими уровнями. На тех уровнях, когда начинается проявление квантовой суперпозиции, согласно которой, система может находиться в нескольких квантовых состояниях одновременно.

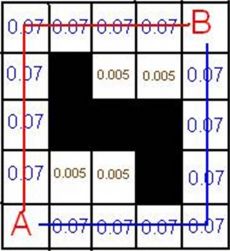
Давайте посмотрим, как справятся с одной практической задачей квантовый и классический компьютеры. Допустим, классическому и квантовому роботу дана задача - сходить в магазин за хлебом. По GPS они получили карту местности и разбили ее на элементарные участки и отметили препятствия. Один из алгоритмов, который позволит роботу найти самый короткий путь из точки «А» (расположение робота) в точку «В» (расположение магазина) - это алгоритм Ли («волновой алгоритм»). Из точки «А» распространяется в 4-х направлениях волна (рис. 2). Элемент, в который пришла волна, образует фронт волны. На рисунках цифрами обозначены номера фронтов волны. Каждый элемент первого фронта волны является источником вторичной волны, каждый второй элемент источником третьей волны и т.д. Построение идет до тех пор, пока волна не достигнет точки «В» и затем, в соответствии с приоритетами, идет построение пути робота (рис.2) таким образом, чтобы при движении от конечного элемента к начальному номер фронта волны (путевые координаты) уменьшались. Посчитаем сколько нужно совершить операций компьютеру, чтобы построить путь из точки «А» в точку «В». Для простоты выберем поле без препятствий, и пусть расстояние между двумя пунктами будет равно 10000. Запишем следующие формулы: a_n=4·n; где a_n– это количество ячеек некоторой волны, n – порядковый номер волны, например у первой волны 4 ячейки, что мы и видим на рисунке. Эта последовательность является арифметической прогрессией, сумма ее членов равна: S_n=(a₁+2(n-1))·n; где S_n- сумма всех ячеек n волн, a₁ – количество ячеек первой волны. Подставляя n=1000, a₁=4, находим, что S_n=200020000. Получается, что для присвоения каждой клеточке своего номера классический компьютер совершает ≈ 2·10⁸ операций. Для современных компьютеров это решаемая задача. Посмотрим, как с этой задачей справиться квантовый компьютер. В силу принципа суперпозиции квантовая система из n кубитов способна одновременно находится в 2ⁿ состояний. Посчитаем, сколько потребуется кубитов, чтобы закодировать каждую ячейку из предыдущей задачи.

2ⁿ=2·10⁸;
n=log₂2·10⁸;
n≈28;

В начальном состоянии у нас имелось 28 обнуленных кубитов. Пусть при некотором воздействии «F1» произошла эволюция связанной системы кубитов таким образом, что их общая волновая функция, при этом:

|ψ>=a₁|0…000>+a₂|0…001>+a₃|0…010>+a₄|0…011>+…+a_S|1…111>; где S=2·10^8, при чем |ψ|²=1 Зададим воздействие «F₁» таким образом, что каждый член суммы a_S|…> кодирует некоторую ячейку по определенному закону. Этим действием мы нумеруем каждую ячейку известным нам образом. Назовем те ячейки, через которые может быть проложен путь из точки «А» в точку «В» «путевыми», а ячейки, через которые кратчайший путь не построить – «лишними». Если мы произведем измерение (считывание) системы кубитов, то обнаружим, что система находится в одном из этих a_S|…> состояний. Причем, вероятность нахождения системы в этом состоянии составляет |a_S|². Сразу после воздействия «F₁» так повлияем на систему кубитов (воздействие «F₂»), чтобы в результате эволюции вероятность нахождения системы кубитов в состояниях, которые отвечают за «путевые» ячейки была максимальной, а в состояниях, которые отвечают за «лишние» ячейки – минимальной (рис.3). Если после операции «F₂» измерять систему кубитов, то наиболее вероятными будут состояния, которые отвечают за «путевые» ячейки. Измерив состояние системы определенное количество раз и обработав полученные данные, можно с некоторой вероятностью найти кратчайший путь из точки «А» в точку «В». Для нахождения пути в 10000 ячеек необходимо, как минимум, произвести 10000 измерений. С циклами обнуления-операция «F1»-операция «F2»-считывание это составит 40000 операций. Для повышения эффективности метода количество измерений, конечно же, должно быть больше, и должна быть система коррекции ошибок. Хоть и быстродействие квантового компьютера на несколько порядков превышает быстродействие классического (40000 против 2·10⁸), для восприятия человека это будет несущественной разницей. Теперь посмотрим, как квантовый и классический компьютер справятся с более сложной задачей. Представим, что два пункта расположены в трехмерном пространстве и нам также необходимо найти кратчайший путь по алгоритму Ли (рис.4). Для каждой волны получаем: a_n=4·n²+2; S_n=(4n³+6n²+8n)/3; Подставляя исходные данные, получаем S_n≈1.33·10¹². Теперь же эта задача доставит классическому компьютеру трудности не только со стороны скорости вычисления, но и со стороны требуемой оперативной памяти. Как же с задачей справиться квантовый компьютер? Найдем количество необходимых кубитов:

2ⁿ=1.33·10¹²;
n=log₂1.33·10¹²;
n≈40;

Общая волновая функция системы кубитов равна: |ψ>=a₁|0…000>+a₂|0…001>+a₃|0…010>+a₄|0…011>+…+a_S|1…111>; где S=1.33·10¹² Несмотря на то, что сейчас пункты «А» и «В» находятся в трехмерном пространстве, путь между ними все также составляет 10000 ячеек и все также необходимо произвести, как минимум, 40000 операций. Вся прелесть такого метода в том, что при измерении выводятся только те ячейки, через которые может проходить путь, а «лишние» ячейки системой кубитов почти не отображаются. Для нахождения пути по квантовому алгоритму будет затрачено минимальное время, и будет необходим гораздо меньший объем оперативной памяти. Как видно, в трехмерной задаче квантовый компьютер имеет существенное преимущество, а в большинстве случаев человеку приходится решать именно многомерные задачи. Представьте себе, как усложниться задача, если на территории находится несколько магазинов, и необходимо брать в расчет не только препятствия на пути движения, но и наличие ассортимента, стоимость товара, его качество, предпочтения хозяина, имеющееся в распоряжении время и т.д. В принципе, огромное число задач, будь то окончить университет, получить специальность, можно представить в виде передвижения от точки «А» в точку «В». Для квантового компьютера решение многомерной задачи придет быстрее, ведь при измерении кубитов, отображаются в основном состояния, которые соответствуют правильному пути. Что это за операция «F2», в результате которой сохраняются все «путевые» ячейки и отбрасываются «лишние»? Я лишь могу предположить, что эту операцию можно задать каким-то математическим образом. Если задуматься, то в нашем мозгу происходит что-то подобное. Мы сначала просто догадываемся, как необходимо решать проблему, а лишь затем находим здравое объяснение своему решению. Я считаю, что понимание, которым мы хотим одарить компьютеры, тесно связано с интуицией и опытом. Опыт является исходными данными и располагаемыми средствами при решении задачи, а интуиция, располагая ими, приводит к верному решению. Для того, чтобы ИИ обладал опытом в определенной области, необходимо производить его обучение. С этим бы отлично справились компьютерные симуляторы, подобные современным играм, которые максимально соответствуют реальности. Квантовый компьютер полностью не заменить классический. Наиболее вероятен их тандем, при котором современный компьютер управляет квантовым и периодически обращается к нему, когда необходимо решить трудную задачу. Для работы квантового компьютера часто требуются экстремальные условия: низкая температура, защита от внешних помех и т.д. Эти условия трудно обеспечить для миллиарда компьютеров. Гораздо выгоднее было бы разместить один большой и мощный квантовый компьютер в одном месте, к которому посредством связи периодически обращались классические. Это бы сильно увеличило производительность компьютеров, и, возможно, было бы первым шагом на пути создания искусственного интеллекта. Человеку не удастся создать ИИ до тех пор, пока он не разберется в себе. Ему необходимо узнать, как рождается мысль, что такое интуиция и что в его мозге отвечает за понимание. В своей работе я хотел показать, что возможно, интуиция, и в какой-то мере понимание, работают на квантовых принципах. И используя особенности квантового мира, можно создать некое подобие искусственного интеллекта.

Используемая литература:

1. Пенроуз Р. Тени разума: в поисках науки о сознании. ­– Москва-­Ижевск: Институт компьютерных исследований, 2005. ­ 688 с.